Intro to Probability and Statistics

Sample Midterm #3 – Questions And Answers (Answer Key)

Professor Brian Shydlo

brian@shydlo.com

Question 1) (12 points) My friend, Marianne, likes to go to Saratoga and bet on the horses.

She would like to bet on the trifecta (also known as the triple) in the first race. In the trifecta, you pick, in order, the first three horses in the race. There are 8 horses in the first race.

Question 1a) (3 points) In order to be certain of winning, Marianne would like to bet on all the trifectas. How many different bets must she place?

Since order matters use the formula for permutations.

Permut(n, r) = n! / (n-r)!

Permut(8, 3) = 8! / (8-3)! = 8! / 5! = 8x7x6x5x4x3x2x1 / 5x4x3x2x1

Cancel out to get 8x7x6x5x4x3x2x1 / 5x4x3x2x1 = 8 x 7 x 6 = 336

The answer is 336

Question 1b) (3 points) She has $500 dollars. Each bet is $2 each. Does she have enough money to bet on all the trifectas?

Each bet is $2. There are 336 different possible bets. So she would need $2 x 336 = $672 to bet on all the possible trifectas. She only has $500.

The answer is No.

Question 1c) (3 points) To box a trifecta means to pick the first three horses of a race, without regard to the order in which they place. How many different boxed trifecta bets are possible for the first race?

Since order does not matter use the formula for combinations.

Combination(n, r) = n! / (r! x (n-r)!)

Combination (8, 3) = 8! / ( 3! x (8-3)! ) = 8! / (3! x 5!) =

8x7x6x5x4x3x2x1 / ( (5x4x3x2x1) x (3 x 2 x 1) )

Cancel out to get (8x7x6x5x4x3x2x1)/ ( (5x4x3x2x1 ) x (3 x 2 x 1) )

= (8 x 7 x 6) / ( 3 x 2 x 1) = (8 x 7 x 6) / ( 6 ) = 56

The answer is 56

Question 1d) (3 points) An exacta (also known as perfecta) is when you pick the first two horses in a race in order. How much money will Marianne have left, if any, is she bets all of the possible boxed trifectas AND bets all the possible exactas? Remember that there are 8 horses, each bet is $2, and Marianne has $500.

As computed in question c, the total number of possible boxed trifectas is 56.

Since order matters for the exacta use the formula for permutations.

Permut(n, r) = n! / (n-r)!

Permut(8, 2) = 8! / (8-2)! = 8! / 6! = 8x7x6x5x4x3x2x1 / 6x5x4x3x2x1

Cancel out to get 8x7x6x5x4x3x2x1 / 6x5x4x3x2x1 = 8 x 7 = 56

The total number of bets is 56 boxed trifectas + 56 exactas = 112 total bets.

The total amount Marianne must spend is 112 x $2 = $224.

She starts with $500, bets $224, so she has $276 left.

So the answer is $276.

Question 2) (12 points) My friend, Jeannie, is an excellent hostess and often invites friends over to her apartment. When she invites people over, she always orders Chinese food. She always orders 8 rolls, 50% spring rolls and 50% Egg Rolls.

Question 2a) (3 points) My friend, Seth, asks me to get him a spring roll from the kitchen. I really can't tell the difference, so I just grab a roll at random and bring it back to Seth. What are the odds that Seth gets the roll that he wants? (Seth can tell the difference)

There is a 50% chance.

Interestingly, whether you use the Hypergeometric Distribution or the Binomial Distribution you get the same answer. The concept of replacement or not replacement doesn't make a difference if you only pick 1 item.

Question 2b) (3 points) Suppose I want to bring back enough rolls to ensure that Seth gets the spring roll that he asked for. (I'll bring the rest back to the kitchen after he selects the spring roll he wants.) What is the fewest number of rolls that I need to bring to ensure that Seth gets a spring roll?

I'd have to bring out exactly 5 rolls.

If I bring out only 4, then there is a chance that all four could be egg rolls.

Interestingly, there is a answer to this because this is a finite population. If this were an infinite population with a binomial distribution, you would need an infinite about to be 100% sure that you get at least one spring roll. For example, even if you pick 100 rolls from your infinite population, with the binomial distribution there is still a 7.89E-31 chance that you won't get a single spring roll. Admittedly that is a very small probability.

Question 2c) (3 points) Suppose I can only carry back three rolls from the kitchen. What are the odds that AT LEAST one of the three is a spring roll?

You would mode this with a hypergeometric distribution. In this case, I bring out 3 rolls. There are 4 possibilities that follow a Hypergeometric Distribution.

Hypergeometric(x, n, M, N) where

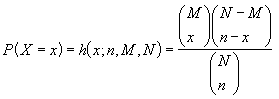
x = Successes in Sample

n = Total Number of sample

M = Successes in Population

N = Total Number in Population

# of Spring Rolls		Probability
0	Hypergeometric(0, 3, 4, 8)	7.14%
1	Hypergeometric(1, 3, 4, 8)	42.86%
2	Hypergeometric(2, 3, 4, 8)	42.86%
3	Hypergeometric(3, 3, 4, 8)	7.14%
Total		100.00%

Since I want at least one to be a spring roll I can either

a) Compute 1 - (the probability of 0 spring rolls) = 100% - 7.14% = 92.86%

or

b) Compute the sum of the probability of 1 spring roll + the probability of 2 spring rolls + the probability of 3 spring rolls = 42.86% + 42.86% + 7.14% = 92.86%

The answer is 92.86%

Several people incorrectly used the binomial distribution. I can't think of a better way to explain why it is dependent when I take rolls and don't replace them. The only think I can think of is to ask what are the odds that I pick 5 rolls and all of them are spring rolls. I think most people would know that the odds are 0, since there are only 4 Spring Rolls in the pile. If this was independent and followed binomial distribution, the odds would be greater than zero.

What Follows is a comparison of the odds if it were binomial compared to Hypergeometric.

For Binomial, assume 3 trials. The odds of pulling a spring roll are 50%. And after I pull a single roll I replace it back into the pile of roll.

For Hypergeometric assume I pull 3 rolls from 8 where 4 are success and 4 are failure.

# of Spring Rolls (Successes)	Hypergeometric Probability	Binomial Probability
0	7.14%	12.50%
1	42.86%	37.50%
2	42.86%	37.50%
3	7.14%	12.50%
Total	100.00%	100.00%

Same things again, but now assume 4 trials for Binomial (p = 50%) or grab 4 rolls for Hypergeometric.

# of Spring Rolls (Successes)	Hypergeometric Probability	Binomial Probability
0	1.4286%	6.25%
1	22.8571%	25.00%
2	51.4286%	37.50%
3	22.8571%	25.00%
4	1.4286%	6.25%
Total	100.00%	100.00%

Same things again, but now assume 5 trials for Binomial (p = 50%) or grab 5 rolls for Hypergeometric.

# of Spring Rolls (Successes)	Hypergeometric Probability	Binomial Probability
0	0*	3.13%
1	7.14%	15.63%
2	42.86%	31.25%
3	42.86%	31.25%
4	7.14%	15.63%
5	0**	3.13%
Total	100.00%	100.00%

* Why is the odds of getting 0 spring rolls without replacement 0% when I pick 5 rolls? Almost everyone got question 2b correct. Question 2b, restated, says that there is a 100% change of getting one or more spring rolls if you take 5 rolls. That means there is a zero chance of picking 0 spring rolls. This makes sense as there are only 4 eggs rolls in the pile.

** Why is the odds of picking 5 spring rolls without replacement 0%? There are only 4 spring rolls in the pile.

Same things again, but now assume 6 trials for Binomial (p = 50%) or grab 6 rolls for Hypergeometric.

# of Spring Rolls (Successes)	Hypergeometric Probability	Binomial Probability
0	0%	1.56%
1	0%	9.38%
2	21.43%	23.44%
3	57.14%	31.25%
4	21.43%	23.44%
5	0%	9.38%
6	0%	1.56%
Total	100.00%	100.00%

If I pick six rolls it should be clear that I can't pick more than 4 spring rolls without replacement. There are only 6 rolls in the pile.

Why can't I pick fewer than 2? If I pick 1 spring roll, then I must have picked 5 egg rolls, which can't be, since there are only 4 in the pile.

Same things again, but now assume 7 trials for Binomial (p = 50%) or grab 7 rolls for Hypergeometric.

# of Spring Rolls (Successes)	Hypergeometric Probability	Binomial Probability
0	0%	0.78%
1	0%	5.47%
2	0%	16.41%
3	50%	27.34%
4	50%	27.34%
5	0%	16.41%
6	0%	5.47%
7	0%	0.78%
Total	100.00%	100.00%

Same things again, but now assume 7 trials for Binomial (p = 50%) or grab 7 rolls for Hypergeometric.

# of Spring Rolls (Successes)	Hypergeometric Probability	Binomial Probability
0	0%	0.78%
1	0%	5.47%
2	0%	16.41%
3	50%	27.34%
4	50%	27.34%
5	0%	16.41%
6	0%	5.47%
7	0%	0.78%
Total	100.00%	100.00%

Same things again, but now assume 8 trials for Binomial (p = 50%) or grab 8 rolls for Hypergeometric.

# of Spring Rolls (Successes)	Hypergeometric Probability	Binomial Probability
0	0%	0.39%
1	0%	3.13%
2	0%	10.94%
3	0%	21.88%
4	100%	27.34%
5	0%	21.88%
6	0%	10.94%
7	0%	3.13%
8	0%	0.39%
Total	100.00%	100.00%

Question 2d) (3 points) Suppose I can only carry back three rolls from the kitchen. What are the odds that EXACTLY one of the three is a spring roll?

See the answer from part c.

The answer is 42.86%

Question 3) (23 points) My friend, Kaplan, is an excellent student. The odds of him getting an A in any class he takes are 95%. There is a 5% chance of him getting a B. There are no other grades he can get. He is in the MBA program at Stern. There are 20 classes that he'll take to graduate.

Question 3a) (4 points) What are the odds that Kaplan will graduate with a 4.00 average? Assume that the grade he gets in each class is INDEPENDENT.

This should be modeled using the Binomial Distribution.

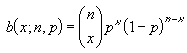
You can approach this one of two ways.

Way 1)

Define p = the probability that Kaplan will get an A = 95%

q = 1 - p = 5%

Number of Trials = 20

Number of successes = 20 (He gets all As)

(20 choose 20) x 0.95²⁰ x 0.05⁰ = 1 x 0.95²⁰ x 1 = 35.85%

Way 2)

Define p = the probability that Kaplan will get a B = 5%

q = 1 - p = 95%

Number of Trials = 20

Number of successes = 0 (He does not get any Bs)

(20 choose 0) x 0.05⁰ x 0.95²⁰ = 1 x 1 x 0.95²⁰ = 35.85%

The answer is 35.85%.

Question 3b) (4 points) What is the expected number of As that Kaplan will get?

The formula for the binomial distribution is np. n = 20. p = 95%.

n x p = 20 x .95 = 19

The answer is 19.

Question 3c) (4 points) My friend Rich is also very smart and is also in the MBA program. He has a 90% chance of getting an A in any given class. What are the odds that Rich will get a better grade than Kaplan in any single class? Remember, there are only two grades, A and Not A (otherwise known as getting a B) and everything is INDEPENDENT.

Hint: Use a Probability Box to get the answer (you don't have to use a box, if you don't need to).

Let:

A = Kaplan gets an A

A' = Kaplan gets a B (does not get an A)

B = Rich gets an A

B' = Rich gets a B (does not get an A)

P(A) = 95% (given in problem)

P(A') = 1 - P(A) = 1 - 95% = 5%

P(B) = 90% (given in problem)

P(B') = 1 - P(B) = 1 - 90% = 10%

Since they are independent we can use the following formula:

The probability Rich gets an A and Kaplan gets a B:

P(A' ∩ B) = P(A') * P(B) = 5% x 90% = 4.5%

Here is the Box

	B	B'
A	85.5%	9.5%	95%
A'	4.5%	0.5%	5%
	90%	10%	100%

The answer is 4.5%.

Question 3d) (4 points) What are the odds that Rich will graduate with a 4.00 average? Assume that the grade he gets in each class is INDEPENDENT and that there are 20 classes.

See the answer to question 3a)

Define p = the probability that Rich will get an A = 90%

q = 1 - p = 10%

Number of Trials = 20

Number of successes = 20 (He gets all As)

(20 choose 20) x 0.90²⁰ x 0.05⁰ = 1 x 0.90²⁰ x 1 = 12.16%

The answer is 12.16%.

Question 3e) (4 points) What are the odds that Rich will graduate with a 4.00 average AND Kaplan will NOT graduate with a 4.00 Average? Assume independence for everything. Remember they each take 20 courses.

Hint 1: This can be solved the same way as question 3c.

Hint 2: I am not asking what are the odds that Rich will graduate with a higher GPA than Kaplan, which is a different question.

Let:

A = Kaplan gets a 4.0

A' = Kaplan does not get a 4.0 (gets less than a 4.0, since you can't get more than a 4.0)

B = Rich gets a 4.0

B' = Rich does not get a 4.0 (gets less than a 4.0, since you can't get more than a 4.0)

P(A) = 35.85% (see part a)

P(A') = 1 - P(A) = 1 - 35.85% = 64.15%

P(B) = 12.16% (see part d)

P(B') = 1 - P(B) = 1 - 12.16% = 87.84%

Since they are independent we can use the following formula:

The probability Rich gets a 4.0 and Kaplan does not?

P(A' ∩ B) = P(A') * P(B) = 64.15% x 12.16% = 7.80%

Here is the Box

	B	B'
A	4.36%	31.49%	35.85%
A'	7.8%	56.35%	64.15%
	12.16%	87.84%	100%

The answer is 7.8%.

Question 3f) (3 points) Assume that at the end of the program Rich has a 4.0 and Kaplan does not. Should Kaplan be upset? What should Kaplan say if Rich gloats about his success (not that Rich would)?

You'll get credit for anything reasonable you write for this question.

This is only an example: Kaplan might say to Rich, "You just got lucky".

Question 4) (8 points) You have 4 dice. Each is a normal six-sided die with a 1/6 probability of landing on each of the sides. You roll all 4 die and add up the scores. So the lowest possible score is 4, in which case you got all 1s and the highest possible score is 24, in which case you must have rolled all 6s.

Question 4a) (4 points) What is the expected value of the sum of the 4 die?

The expected value of a single die is (1 + 2 + 3 + 4 + 5 + 6) / 6 = 3.5

The expected value of 4 dice is 4 * 3.5 = 14

The answer is 14.

Question 4b) (4 points) What is the Variance of the sum of the 4 die?

Hint: The Standard Deviation of a single die is 1.708.

Let Var(X₁) be the variance for Die 1.

Let Var(X₂) be the variance for Die 2.

Let Var(X₃) be the variance for Die 3.

Let Var(X₄) be the variance for Die 4.

The variance of each one is the square of the standard deviation: 1.708 * 1.708 = 2.917.

The variance of a sum is the sum of the variances (only if they are independent, which they are in this case) so:

Var ( X₁ + X₂ + X₃ + X₄) = 2.917 + 2.917 + 2.917 + 2.917 = 11.668

The answer is 11.668.

Question 5) (21 points) Assume that you have a portfolio of 7 Bonds in total. You have 3 B rated bonds and 4 D rated bonds. The following chart will be the default rate for those bonds. Assume that all defaults of B relative to D bonds are INDEPENDENT.

B Bonds

# Defaults	Probability
0	50%
1	35%
2	10%
3	5%

D Bonds

# Defaults	Probability
0	1%
1	5%
2	10%
3	30%
4	54%

Question 5a) (4 points) What is expected value of the number of defaults for B bonds?

# Defaults	Probability	Probability * (# of Defaults)
0	50%	0.00
1	35%	0.35
2	10%	0.20
3	5%	0.15

Answer = 0 x 50% + 1 x 35% + 2 x 10% + 3 x 5% = 0.70

The answer is 0.70.

Question 5b) (4 points) What is variance and standard deviation of the number of defaults for B bonds?

# Defaults	Probability	Expected Value	Deviation	Squared Deviation	Squared Deviation x Probability
0	50%	0.70	-0.7	0.49	0.2450
1	35%	0.70	0.3	0.09	0.0315
2	10%	0.70	1.3	1.69	0.1690
3	5%	0.70	2.3	5.29	0.2645

Answer = 0.2450 + 0.0315 + 0.1690 + 0.2645 = 0.71

Take square root of 0.71 to get the standard deviation = 0.843

The answer is 0.71 for Variance and 0.843 for the standard deviation.

Question 5c) (3 points) What are the odds that you get exactly 0 defaults in your whole portfolio?

So you get 0 B rated bonds defaulting and 0 D rated bonds defaulting.

Hint: I am looking for the Intersection

Let:

A = 0 B bonds default

B = 0 D bonds default

There are independent so you can use this formula:

P(A ∩ B) = P(A) * P(B) = 50% x 1% = 0.50%

The answer is 0.50%

Question 5d) (3 points) What are the odds that you get 0 B rated bond defaults or 0 D rated bond defaults (or 0 total defaults).

Hint: I am looking for the Union

Let:

A = 0 B bonds default

B = 0 D bonds default

Use the formula:

P(A U B) = P(A) + P(B) - P(A ∩ B)

P(A ∩ B) = 0.50%, computed in question 5c

50.5% = 50% + 1% - 0.5%

The answer is 50.5%

Question 5e) (4 points) What are the odds that you get exactly 1 default in your whole portfolio?

So you get 1 B rated bond defaulting and 0 D rated bonds defaulting OR

So you get 0 B rated bond defaulting and 1 D rated bonds defaulting.

Let:

B₀ = 0 B Bonds default

B₁ = 1 B Bond default

D₀ = 0 D Bonds default

D₁ = 1 D Bond default

P(B₀) = 50%

P(B₁) = 35%

P(D₀) = 1%

P(D₁₎ = 5%

Since they are independent we can use the following formula:

P(B₀ ∩ D₁) = P(B₀) * P(D₁) = 50% x 5% = 2.50%

P(B₁ ∩ D₀) = P(B₁) * P(D₀) = 35% x 1% = 0.35%

P(B₀ ∩ D₁) + P(B₁ ∩ D₀) = 2.50% + 0.35% = 2.85%

The answer is 2.85%.

Question 5f) (3 points) Assume that you have a portfolio of 7 Bonds in total. You have 3 B rated bonds and 4 D rated bonds. (same as before so far) Now assume that the bond defaults are binomially distributed.

p_B-Bond = the probability that a B rated bond defaults = 20%

p_D-Bond = the probability that a D rated bond defaults = 90%

Fill in the chart using the binomial distribution odds:

B Bonds

# Defaults	Probability
0	0.5120
1	0.3840
2	0.0960
3	0.0080

D Bonds

# Defaults	Probability
0	0.0001
1	0.0036
2	0.0486
3	0.2916
4	0.6561

Question 6) (24 points) My friend Tony has a width of 15 inches. (Don't confuse width with waist size, which would be diameter x pi = (15 inches * 3.14) if Tony's waist was a perfect circle.)

A person's width is normally distributed with a mean of 12 inches and a standard deviation of 1.5 inches.

The seats at a Broadway show are exactly 14 inches wide. Anyone who comes to a show who is greater than 14 inches wide will be uncomfortable. Anyone who comes to the show who is exactly 14 inches or less will be comfortable.

Question 6a) (3 points) Suppose Tony goes to the theater above. What are the odds that he will be uncomfortable?

The answer is 100%.

Question 6b) (6 points) A random person comes into the theater. This person's width follows the normal distribution as described above. What are the odds that this person will be uncomfortable?

Step one: Do Z transformation to figure out standard deviations from the mean.

(14 - 12) / 1.5 = 1.333

What is the probability that a person's width is greater than 1.333 standard deviations from the mean?

Look up on the chart of standard normal distributions (which assume a mean of zero and a standard deviation of 1).

You see 40.8789%

This means that from 0 to 1.333 standard deviations there is a 40.8789% chance.

We know that from -infinity to 0 there is a 50% chance.

So total to the left of 1.333 standard deviations is 90.8789%.

We want greater than 2 standard deviations so its 100% - 90.8789% = 9.1211%

The answer is 9.1211%.

Question 6c) (6 points) A person is ultra-comfortable if they have 3 or more inches of extra room in their chair. Assume that a random person comes into the theater. This person's width follows the normal distribution as described above and the chairs are 14-inches wide. What are the odds that this person will be ultra-comfortable?

Since the chairs are 14 inches wide, a person would need to be (14 - 3) = 11 inches wide or less than 11 wide to be ultra-comfortable.

Do Z transformation to figure out standard deviations from the mean.

(11 - 12) / 1.5 = -0.66666

What is the probability that a person's width is less than -0.666 standard deviations from the mean?

Look up on the chart of standard normal distributions (which assume a mean of zero and a standard deviation of 1).

We know that the distribution is symmetric so we can look up +0.666 instead of -0.666.

You see 24.75%

This means that from 0 to 0.666 standard deviations there is a 24.75% chance.

We know that from 0 to infinity there is a 50% chance.

So total to the right of 0.666 standard deviations is 25.25%.

This means that to the left of -0.666 is also 25.25%.

The answer is 25.25%.

Question 6d) (3 points) Assume that a particular theater on Broadway has 10 rows of seats, each of the 10 rows is 70 feet across. Each seat is exactly 14 inches wide and there are no gaps or aisles between the seats. The theater fills up every night and they charge $50 per seat. How much money do they make each night?

70 feet across / 12 inches/foot = 840 inches across

840 inches / 14 inches/seat = 60 seats

60 seats/row * 10 rows = 600 seats

600 seats * $50/seat = $30,000

The answer is $30,000.

Question 6e) (3 points) Assume that the owner of the theater can at zero cost switch to seats that are 15 inches wide. How much money will they lose relative to the 14 inch wide seats? Assume that they fill up the theater with either size seat.

First figure out how much they make with 15 inch seats

70 feet across / 12 inches/foot = 840 inches across

840 inches / 15 inches/seat = 56 seats

56 seats/row * 10 rows = 560 seats

560 seats * $50/seat = $28,000

$30,000 - $28,000 = $2,000

The answer is $2,000.

Question 6f) (3 points) More seats mean more money when you assume that the theater is always full. That assumption will not hold if the seats get too small. People will not be comfortable and not go to your theater.

What sort of analysis would you do to determine the optimal size of seats in your theater assuming you want to maximize profits? What do you tell Tony if he complains that the seats are uncomfortable?

Any reasonable answer will be accepted and there are several approaches you can take.

You may want to set the seat size so that if

a) You make the seats a little bigger you would lose money from fewer seats.

b) You make the seats a little smaller you would lose money from fewer customers (you have more seats, but they are empty because people don't go to your theater).

You might do an analysis like this:

Seat Width	70*12*10 = Inches to place seats	Total Seats	Per Seat Profit	Revenue if Full house = Seats * $50	Estimated Revenue Based on my guess
6	8400	1400.00	$ 50.00	$70,000.00	$ -
7	8400	1200.00	$ 50.00	$60,000.00	$ 50.00
8	8400	1050.00	$ 50.00	$52,500.00	$ 1,000.00
9	8400	933.33	$ 50.00	$46,666.67	$ 5,000.00
10	8400	840.00	$ 50.00	$42,000.00	$15,000.00
11	8400	763.64	$ 50.00	$38,181.82	$20,000.00
12	8400	700.00	$ 50.00	$35,000.00	$25,000.00
13	8400	646.15	$ 50.00	$32,307.69	$27,900.00
14	8400	600.00	$ 50.00	$30,000.00	$29,000.00
15	8400	560.00	$ 50.00	$28,000.00	$28,000.00
16	8400	525.00	$ 50.00	$26,250.00	$26,250.00
17	8400	494.12	$ 50.00	$24,705.88	$24,705.88
18	8400	466.67	$ 50.00	$23,333.33	$23,333.33
19	8400	442.11	$ 50.00	$22,105.26	$22,105.26
20	8400	420.00	$ 50.00	$21,000.00	$21,000.00

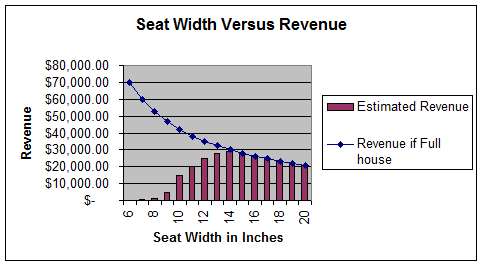
So even though you might want to shrink seats to make more profit, if you actually make the seats 7 inches wide, you only make $50 profit, not the $60,000 you might have naively expected.